Член геометрической прогрессии

Ученикам может показаться, что изучение геометрической прогрессии — это нечто абстрактное и оторванное от жизни. На самом деле множество экономических процессов построены именно на основе геометрической прогрессии. Например, если вы положите деньги на банковский депозит и захотите посчитать сколько процентов заработаете за три года, самым удобным способом провести вычисления будет именно через формулу геометрической прогрессии.

Занятие3. Геометрическая прогрессия

Геометрической прогрессией называется последовательность, в которой первый член отличен от нуля, а каждый из последующих равен предыдущему, умноженному на некоторое постоянное для данной последовательности число, отличное от нуля. Это число называется знаменателем геометрической прогрессии q геометрической прогрессии. Геометрическая прогрессия задаётся своим первым членом и знаменателем.

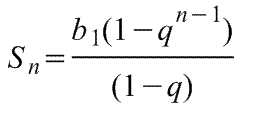
Рассмотрим последовательность, членами которой являются степени числа два с натуральными показателями: два, два квадрат, два куб, два четвертой степени и так далее. Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на два. Эта последовательность является примером геометрической прогрессии. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

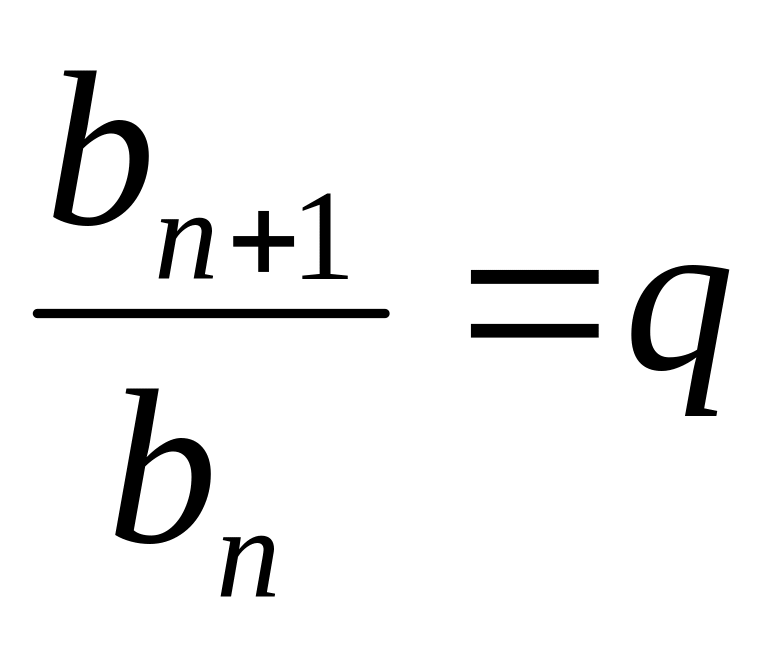
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Попробуйте онлайн калькуляторы для вычисления прогрессий Значение n-того члена арифметической прогрессии Сумма арифметической прогрессии Показать все онлайн калькуляторы.

Похожие статьи

• Пизда и большой член
• Порно бабы без сознания от гигантских членов
• Фото а ты подрочи мой член
• Порно аня получила член в попу